The thermodynamic properties of surface tension and density play a crucial role in phenomena such as gas absorption, distillation, crystallization, melting, fusion, and evaporation. These properties are also pivotal in various industries including rubber, plastic, and paint manufacturing. Surface tension in liquids and gases is essential for studying interfacial surfaces and understanding the nature of reactions within mixtures.
Surface tension manifests in two states: on exposed surfaces, it tends to contract, reducing the surface area as liquid molecules draw closer together with force; on unexposed surfaces, it tends to expand, causing molecules to move apart. Although extensive study of surface tension is challenging, it has been examined under critical temperature conditions. Surface tension is defined as the energy required transferring a portion of the liquid mass to the surface to increase the surface area.
The complex structure of binary systems makes it difficult to obtain surface tension data due to temperature and prolonged experimental measurements. Thermo-dynamic properties are calculated to alter the characteristics of colloidal systems, driven by technological advancements and the need to enhance the application of metals through understanding their physical properties.
Experimental systems are maintained with a density greater than that of Boyle's density and temperatures below twice the boiling point. The Cahn–Hilliard (CH) theory is employed to calculate physical parameters in polymers, providing a simple model for the structure of multi-phase polymer materials. This theory examines the structure of polymer materials to understand changes in mass and surface tension.
Physical parameters are studied as a function of temperature to express surface tension, gradient energy coefficient, density, and reduction in surface tension.
Cahn–Hilliard Theory
Physical parameters in polymers are calculated using the Cahn–Hilliard (CH) theory, a simple model for the structure of multi-phase polymer materials. The theory examines how mass and surface tension change in polymer materials.
 (1)
(1)
 : represents the energy density of a homogeneous polymer and is represented by the Laplace equation and density in the following relationship.
: represents the energy density of a homogeneous polymer and is represented by the Laplace equation and density in the following relationship.
 ,
,  (2)
(2)
The symbol (o) in Equation 2 refers to the finite derivatives in gradient energy density  and
and  tends to zero. The free energy A of the system volume is V determined by Equation 3:
tends to zero. The free energy A of the system volume is V determined by Equation 3:
 (3)
(3)
k: The gradient energy coefficient [10] and the theoretical values for the low gradient energy coefficient (k =0.5 ) were calculated by Sutherland. The first term in Equation 3 represents the Helmholtz free energy of a homogeneous polymer, while the second term represents the gradient energy coefficient in the free energy.
 (4)
(4)
 : represents the difference between the free energy of homogeneous and heterogeneous polymers (liquid and gas) as shown below.
: represents the difference between the free energy of homogeneous and heterogeneous polymers (liquid and gas) as shown below.
 (5)
(5)
 ,
,  The chemical potentials of liquid and vapor in equilibrium are derived in detail [7], indicating a reduction in surface tension and low gradient energy coefficient.
The chemical potentials of liquid and vapor in equilibrium are derived in detail [7], indicating a reduction in surface tension and low gradient energy coefficient.
 ,
,  ,
,  (6)
(6)
The characteristic arrangement of holes and molecules is determined by the Flory–Huggins theory and can be measured by mixing a set of entropies of holes and molecules using the Boltzmann constant.
 (7)
(7)
Simha-Somcynsky (SS) Theory
The Simha-Somcynsky (SS) theory describes the cell structure, assuming that cells and unoccupied molecules exist in the lattice cell due to the instability of liquid and solid polymers. Here, y refers to the occupied part location.
 (8)
(8)
The partition function [16] indicates the location of the filled and free volume part, as shown below:
 (9)
(9)
All lattice energies [17], unconstrained volumes, and values of harmonic factors are implemented. This remains unchanged in system equilibrium when the derivative equals zero according to the work rate.

 (10)
(10)

We will obtain the equation of state [18] by deriving the Helmholtz free energy for the polymer system to calculate pressure and volume at specific temperatures [19].
 (11)
(11)

 (12)
(12)
The PVT relationship refers to the relationship between Equation (7) and Equation (8) [20].
 ,
,  (13)
(13)
The physical parameters shown in Equation (9) are P*, V*, T*
 ,
,  ,
,  (14)
(14)
Entropy and chemical force substitution in binary systems, free energy function parameters, and derivation procedures [21]. The chemical potential is the difference between mass and surfaces.
 (15)
(15)
 Are refer to the location of the occupied part for large and superficial quantities, respectively, formulating the free energy by potential difference. The Scaled Helmholtz energy is expressed by chemical potential difference as:
Are refer to the location of the occupied part for large and superficial quantities, respectively, formulating the free energy by potential difference. The Scaled Helmholtz energy is expressed by chemical potential difference as:
 (16)
(16)
 (17)
(17)


 (18)
(18)
Measurement variables
 ,
, 
 ,
,  (19)
(19)
 (20)
(20)
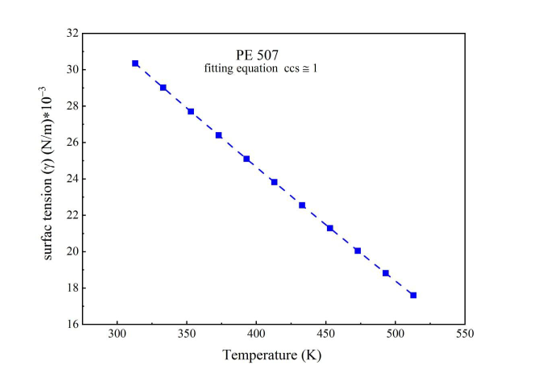
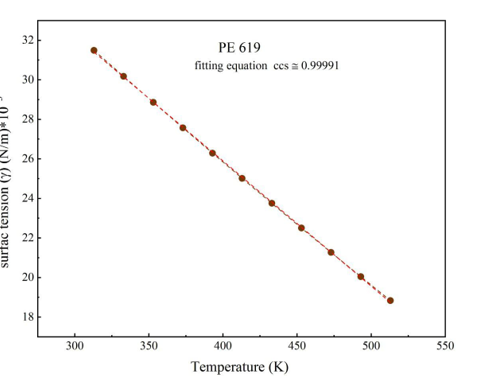
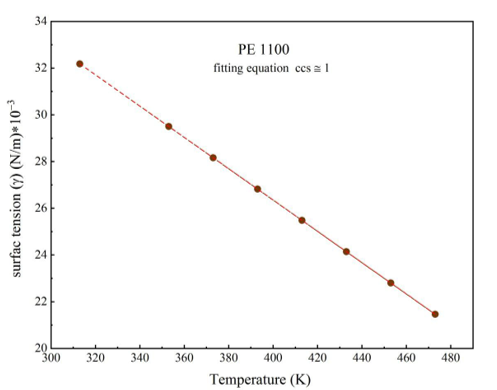
Equations 19 and 6 are used to calculate temperature and pressure to find the surface tension coefficient and low gradient energy coefficient for PE198, PE507, PE619, and PE1100. The temperatures start from 313K to 513K and pressures from 0.1 MPa to 150 MPa, respectively, to illustrate the change in coefficients from volume to surface.
Surface tension is described as a force [22], withxymers are stable. These experimental results are calculated to apply the SS theory to understand physical parameters (P*, V*, T*, c/s ) in Equations 10 and 12. Each part repeated in the polymer can be considered as land and building. The total freedom of polymers (s) is 3c, where (c) represents the least volumetric error in PVT data [23-24]. Experimental data from the SS theory can be found from Equations 12 and 10 and can be matched with experimental data using the CH theory and the parameters in Tables 1, 2, 3, and 4.